对于简单的变换, 我们可以用数学表达式实现(参考三角函数), 但是当情况变得复杂的时候, 我们就需要用 变换矩阵(Transformation matrix) 来完成这项工作, 变换矩阵非常适合操作计算机图形.
变换矩阵: 旋转
示例矩阵:
8 3 0
4 3 6
3 2 6
再解释如何用变换矩阵来替代数学表达式之前, 我们需要理解矩阵和矢量的乘法, 矢量就是由多个分量组成的对象,比如顶点的坐标(0.0,0.5,1.0)
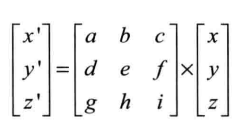
上式中的这个矩阵具有3 行 3 列,因此又被称为3×3 矩阵. 矩阵右侧是一个由x、y、 z组成的矢量 (为了与矢量相乘,矢量被写成列的形式,其仍然表示点的坐标), 矢量具有 3个分量, 因此被称为三维矢量. 再次说明, 数字两侧的方括号表示这些数字是一个整体(一个矢量)
矩阵与矢量想成得到的新矢量, 其三个分量 x’ y’ z’ 等式如下图所示:
x' = ax + by + cz
y' = dx + ey + fz
z' = gx + hy + iz
中间经过了一堆sincos没看懂的(P99页), 反正最后旋转矩阵可以表现为:
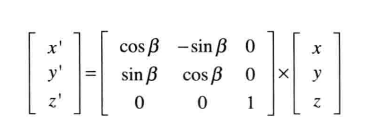
这个矩阵就被称为 变换矩阵(transformation matrix), 因为它将右侧的矢量 (x, y, z) 变换为了左侧的矢量 (x', y', z'), 上面的矩形变换的是一次旋转, 所以我们就这样迷迷糊糊的讲了一个旋转矩阵(rotation matrix)
变换矩阵: 平移
如果我们能用变换矩阵来表示旋转, 那么我们也就能用它来表示其他变换, 比如平移
在平移中我们使用 4 x 4的矩阵, 和具有第四个分量**(一般都是1.0)**的矢量, 假设 P 点坐标为 (x, y, z, 1), 平移之后的点 p’ 坐标为 (x', y', z', 1), 等式如下:

矩阵乘法表示如下:
x' = ax + by + cz + d
y' = ex + fy + gz + h
z' = ix + jy + kz + p
1 = mx + ny + oz + p
根据最后一个式子1 = mx + ny + oz + p , 很容易求算出系数 m = 0, n = 0, o = 0, p = 1
中间经过了一堆没看懂的, 反正最后平移矩阵可以表现为: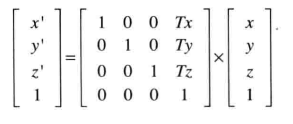
4 x 4 的旋转矩阵
前面讲了一个平移矩阵和一个旋转矩阵, 两个矩阵的作用是一样的, 就是 计算变换后的顶点坐标 在 先旋转再平移 的情形下, 我们将最后的矩阵整合起来, 然后就变成了这么个模样
还是直接上代码吧
https://github.com/bajiu/blog_code/blob/master/webGL/class/class_06.js

