高斯分布

高斯分布，也称为正态分布，是统计学中最重要的概率分布之一。其数学形式简洁且在自然和社会科学中广泛应用。高斯分布的基本特性和概念包括：

数学表达式

高斯分布的概率密度函数（PDF）为：

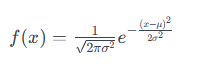
formula

其中，x 是变量，μ 表示分布的均值，σ 表示标准差，σ平方 （不会打平方）是方差

图形特征

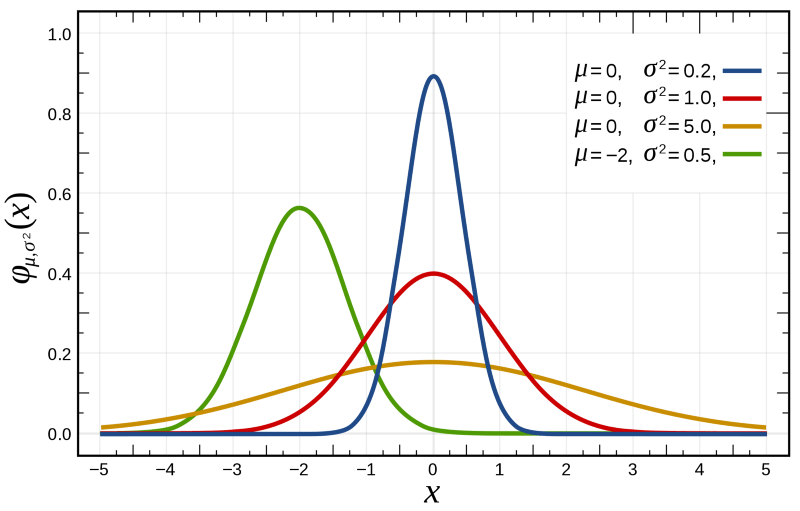
钟形曲线：高斯分布在均值附近最高，随着距离均值的增加，概率密度逐渐减小，形成钟形。
对称性：关于均值 μ 对称。

标准正态分布
当 μ=0 且 σ=1 时，高斯分布成为标准正态分布，简化为：

detail

标准正态分布在统计理论中非常重要，许多统计方法都基于或与之相关。

代码实现

函数会接收一个值 x，以及分布的均值（μ）和标准差（σ），然后根据高斯分布的公式返回该值的概率密度。一个简单的 C# 实现：

using System;

class GaussianDistribution
{
    // 计算高斯分布的概率密度函数
    public static double ProbabilityDensityFunction(double x, double mean, double stdDev)
    {
        double exponent = Math.Exp(-0.5 * Math.Pow((x - mean) / stdDev, 2));
        return (1 / (stdDev * Math.Sqrt(2 * Math.PI))) * exponent;
    }

    static void Main(string[] args)
    {
        double mean = 0;   // 均值 μ
        double stdDev = 1; // 标准差 σ

        // 示例：计算高斯分布在不同 x 值的概率密度
        Console.WriteLine("Probability Density of Gaussian Distribution:");
        for (double x = -3; x <= 3; x += 0.5)
        {
            double pdf = ProbabilityDensityFunction(x, mean, stdDev);
            Console.WriteLine($"x = {x}, PDF = {pdf}");
        }
    }
}

高斯分布的性质

中心极限定理：许多独立随机变量之和（或平均值）在一定条件下趋近于正态分布，即使原始变量本身不是正态分布。
68-95-99.7 规则（又称为经验法则）：在一个正态分布中，约 68% 的数值位于距均值一个标准差的范围内，约 95% 的数值位于距均值两个标准差的范围内，而约 99.7% 的数值位于距均值三个标准差的范围内。

高斯分布的局限性

尽管高斯分布非常重要，它不适用于所有类型的数据。例如，对于具有偏斜、多峰、有界或离散特征的数据，其他分布（如泊松分布、指数分布、二项分布）可能更合适。

高斯分布与其他分布的关系

当独立同分布的随机变量数量足够大时，它们的和或平均值趋向于正态分布（中心极限定理）。
正态分布是许多其他分布（如卡方分布、t分布）的基础。

结论

高斯分布之所以重要，是因为它是理解和应用统计分析的基础。它的数学形式简单，且在现实世界中有广泛的应用。理解高斯分布的基本特性和限制对于从事数据分析的人员来说是非常重要的。

bajiu